亲爱的编程爱好者们,今天我要和你聊聊一个神奇的小玩意儿——递归函数。你可能已经在编程的海洋里遨游了一段时间,但递归函数这个概念,就像海底的珍珠,等待你去发现它的光芒。别急,让我带你一步步揭开它的神秘面纱。
什么是递归函数?

想象你正在玩一个猜数字的游戏。我告诉你一个数字,你猜一猜,猜不对再猜一次,直到猜对为止。这个过程,就像是递归函数的缩影。递归函数,简单来说,就是函数在执行过程中调用自己。
递归函数的例子:阶乘
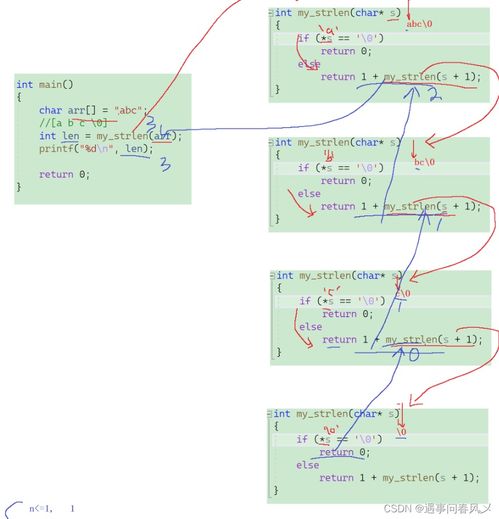
来,我们先从最经典的例子——阶乘说起。阶乘,用数学符号表示就是 n!,意思是 n 乘以 n-1,再乘以 n-2,一直乘到 1。比如,5! 就是 5×4×3×2×1,结果是 120。
现在,让我们用递归函数来计算阶乘。定义一个函数 factorial(n),如果 n 等于 0,就返回 1;否则,返回 n 乘以 factorial(n-1)。这个过程,就像是你在猜数字游戏中,每次猜不对就再猜一次,直到猜对为止。
```python
def factorial(n):
if n == 0:
return 1
else:
return n factorial(n-1)
用这个函数计算 5!,它会这样执行:
1. factorial(5) 调用 factorial(4)
2. factorial(4) 调用 factorial(3)
3. factorial(3) 调用 factorial(2)
4. factorial(2) 调用 factorial(1)
5. factorial(1) 返回 1
6. 回到 factorial(2),得到 2 1 = 2
7. 回到 factorial(3),得到 3 2 = 6
8. 回到 factorial(4),得到 4 6 = 24
9. 回到 factorial(5),得到 5 24 = 120
是不是感觉就像是在玩一个猜数字的游戏,每次猜不对就再猜一次,直到猜对为止?
递归函数的例子:斐波那契数列
斐波那契数列,相信大家都不陌生。它是一个神奇的数列,从第三项开始,每一项都是前两项的和。比如,数列的前几项是 1, 1, 2, 3, 5, 8, 13...
现在,我们用递归函数来计算斐波那契数列的第 n 项。定义一个函数 fibonacci(n),如果 n 小于等于 1,就返回 n;否则,返回 fibonacci(n-1) 加上 fibonacci(n-2)。
```python
def fibonacci(n):
if n <= 1:
return n
else:
return fibonacci(n-1) fibonacci(n-2)
用这个函数计算 fibonacci(5),它会这样执行:
1. fibonacci(5) 返回 fibonacci(4) fibonacci(3)
2. fibonacci(4) 返回 fibonacci(3) fibonacci(2)
3. fibonacci(3) 返回 fibonacci(2) fibonacci(1)
4. fibonacci(2) 返回 fibonacci(1) fibonacci(0)
5. fibonacci(1) 返回 1
6. fibonacci(0) 返回 0
7. 回到 fibonacci(2),得到 1 0 = 1
8. 回到 fibonacci(3),得到 1 1 = 2
9. 回到 fibonacci(4),得到 2 2 = 4
10. 回到 fibonacci(5),得到 4 3 = 7
是不是感觉就像是在玩一个猜数字的游戏,每次猜不对就再猜一次,直到猜对为止?
递归函数的例子:汉诺塔
汉诺塔,是一个古老的数学问题。它要求你将 n 个盘子从一根柱子移动到另一根柱子,同时每次只能移动一个盘子,且大盘子不能放在小盘子上面。
现在,我们用递归函数来解决汉诺塔问题。定义一个函数 hanoi(n, source, target, auxiliary),其中 n 表示盘子的数量,source 表示源柱子,target 表示目标柱子,auxiliary 表示辅助柱子。
```python
def hanoi(n, source, target, auxiliary):
if n > 0:
hanoi(n-1, source, auxiliary, target)
print(f\Move disk {n} from {source} to {target}\)
hanoi(n-1, auxiliary, target, source)
用这个函数解决 n=3 的汉诺塔问题,










